フォントの制御点が多すぎるので減らしてみようという件。

超でもないけど、レアネタ

どういう需要かはさておき、フォントのね。メトリクスのベジェ曲線の制御点がね。多すぎるんですよ。

もともとのつくりなのか、TTFのスプラインからベジェ変換してるのが理由なのかは知りませんが、、

とにかく制御点が多すぎるんですよ。

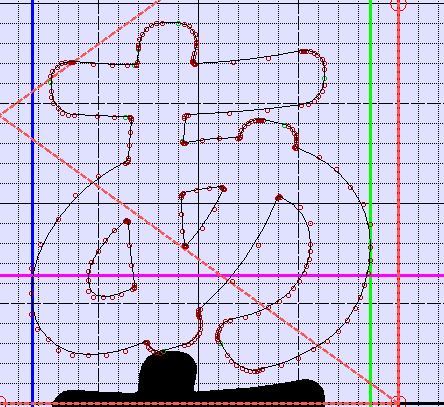
下図をみればわかる通り、これ、【源柔ゴシック Heavy】なんですが、、

まぁ制御点が多いのはこのフォントに限ったことでも無いのですが、

とにかく多すぎです。べじぇ

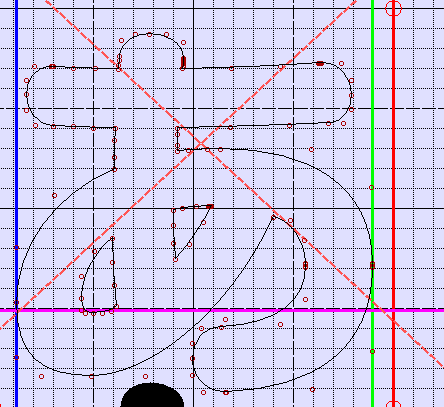
これは、FOT-スーラ Pro EB （＠フォントワークス）ですが、もともとのフォントベンダさんで、

PostScriptフォントを作ってたとこのメトリクスの制御点はこんなもんですよ。

で、何がしたいのか

そう、何がしたいのかと言うと、、

【フォントを図形で描画したくて、その時の制御点を減らしてスピードアップさせたい】

ってことなんです。

何のため？
とか、そういうことはどーでもいいです。^^;

どうするか？

どうする？ってもちろん、

【連続するベジェ曲線がひとつにまとまりそうだったらひとつにする】

【それをLOOPさせて、極限まで減らす】

まぁ、そういうことです。

問題を分類すると、

・実際にまとめるロジック

・”まとまりそう”の判定

実際にまとめるロジックを考える

まとめるロジックは、こんなんでどうでしょね。

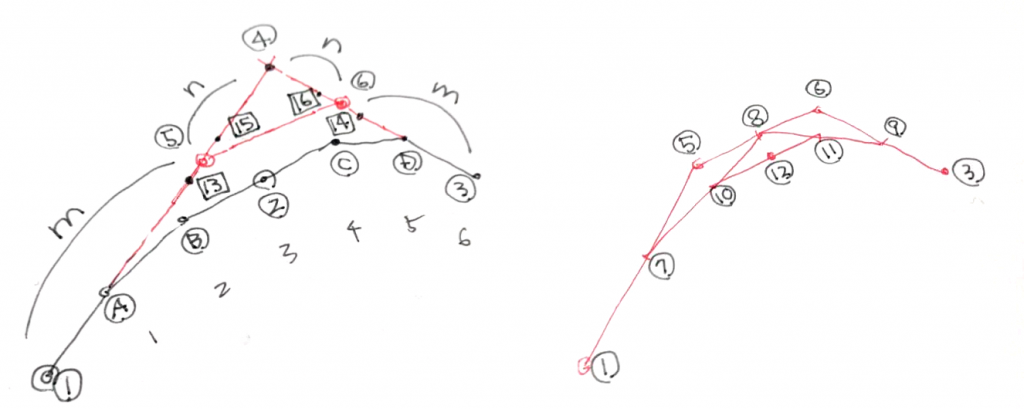
２つのベジェ曲線を、

①-A-B-②　と

②-C-D-③　としますね。

線分①-Aと線分③-Dの交点を④として、

線分①-④をｍ：ｎに内分する点を⑤とし、

線分④-③をｎ：ｍに内分する点を⑥とし、

①開始点-⑤制御点１-⑥制御点２-③
で構成するベジェ曲線を定義します。

そして、ベジェ曲線の性質として、点⑫を通るので（細かい点割愛）、点⑫と点②の距離が近づくようなｍ：ｎを割り出せばよいのではないか！？

という結論です。

もちろん、⑫と②の距離がいいのか、それとも⑫と線分Ｂ-Ｃとの距離がいいのか、、

そこらへんはよくわかってないです。

まぁプログラムとしては３次方程式とかは解きません。

イテレートすればいいかなと。

イテレートはどうするかというと、、

まず、m:nを0~1まで0.1刻みでLOOP。

距離の最小値のm:nを求め、その±0.1の範囲を特定。

次にこの範囲のm2:n2を、0.1刻みでLOOP。

その時のTempolary座標が、13,14,15,16

なんてことをやって、４回LOOPさせれば、10000等分したメッシュの中に入る一番近い点をみつけられるのではないかと。

そう考えると、やっぱ、⑫とB-Cの距離の方がよい気がしますねー。

➡やってみたところ、点と線の距離（垂線の足的に）のほうが良いことがわかりました(o^^o)

まとまりそう判定ロジックを考える

これはわりと簡単です。３つほどあります。

その１：　①－A／A－B／B－②／②－C／C－D／D－③　のなす角度が、ゆるやかかどうか

その２：　①ーA　と　Dー③　の角度が、一定の角度以内になっているかどうか

その３：　①－A－B－②の距離と、②－C－D－③　の距離の比率が一定以内かどうか

あたりですね。

※ゆるやかとか、一定の角度以内というのは、やってみながら決めて行けばよいかなと。

やってみていいかんじでまとまれば、

１：±20deg（但し、途中で反転しないこと）

２：90deg

３：0.667~1.5

くらいになりませんかねーー。

では、、やってみましょう！

やってみた結果。第一回。

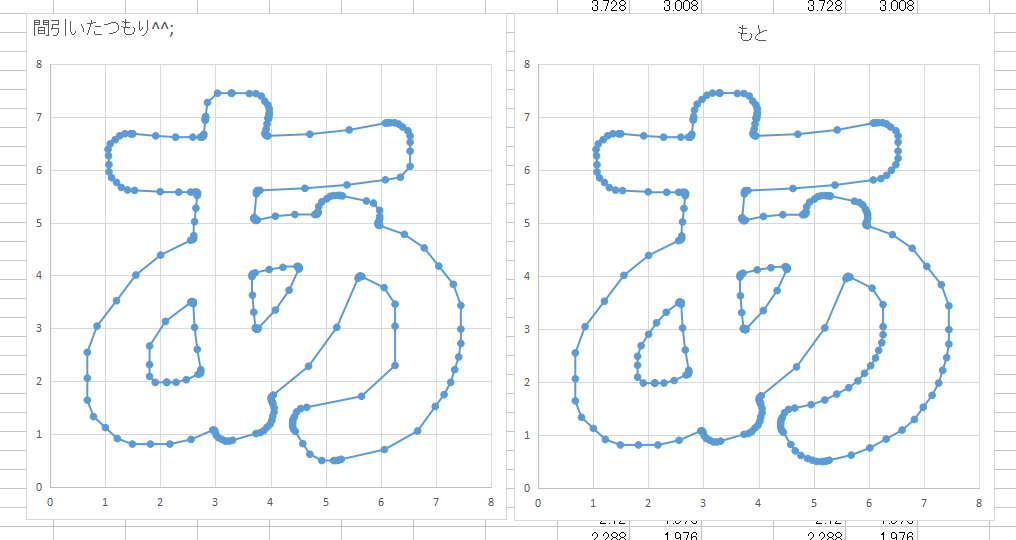
うぅーーん。

思ったほど減ってない。

あ、【間引いたつもり】の左側の方ですが、

カクカクして見えるのは、制御点なので、

実際は曲線になるので心配ありません。(o^^o)

さらなるロジックを追加しないとダメですねー。

例えば、、

本当は直線なのにベジェ指定されてるとか（制御点も含めてほぼ一直線でそれでいてめっちゃ短い線とか）、

特に一画目の初めの部分とか、

二画目の終わりの飛び出してる部分とか、、

めっちゃ気に入りませんよねー。。

つづく。